Real Tips About Can I Connect Square To Wave

Decoding the Connection

1. Understanding the Basics of Waveforms

So, you're pondering whether you can directly "connect" a square wave to a sine wave, eh? Well, the short answer is... it's complicated. Think of it like asking if you can directly connect a brick wall to a bouncy castle. They're both structures, but they behave very differently. Similarly, square waves and sine waves are fundamentally different types of signals. Let's dig a little deeper into what makes them tick.

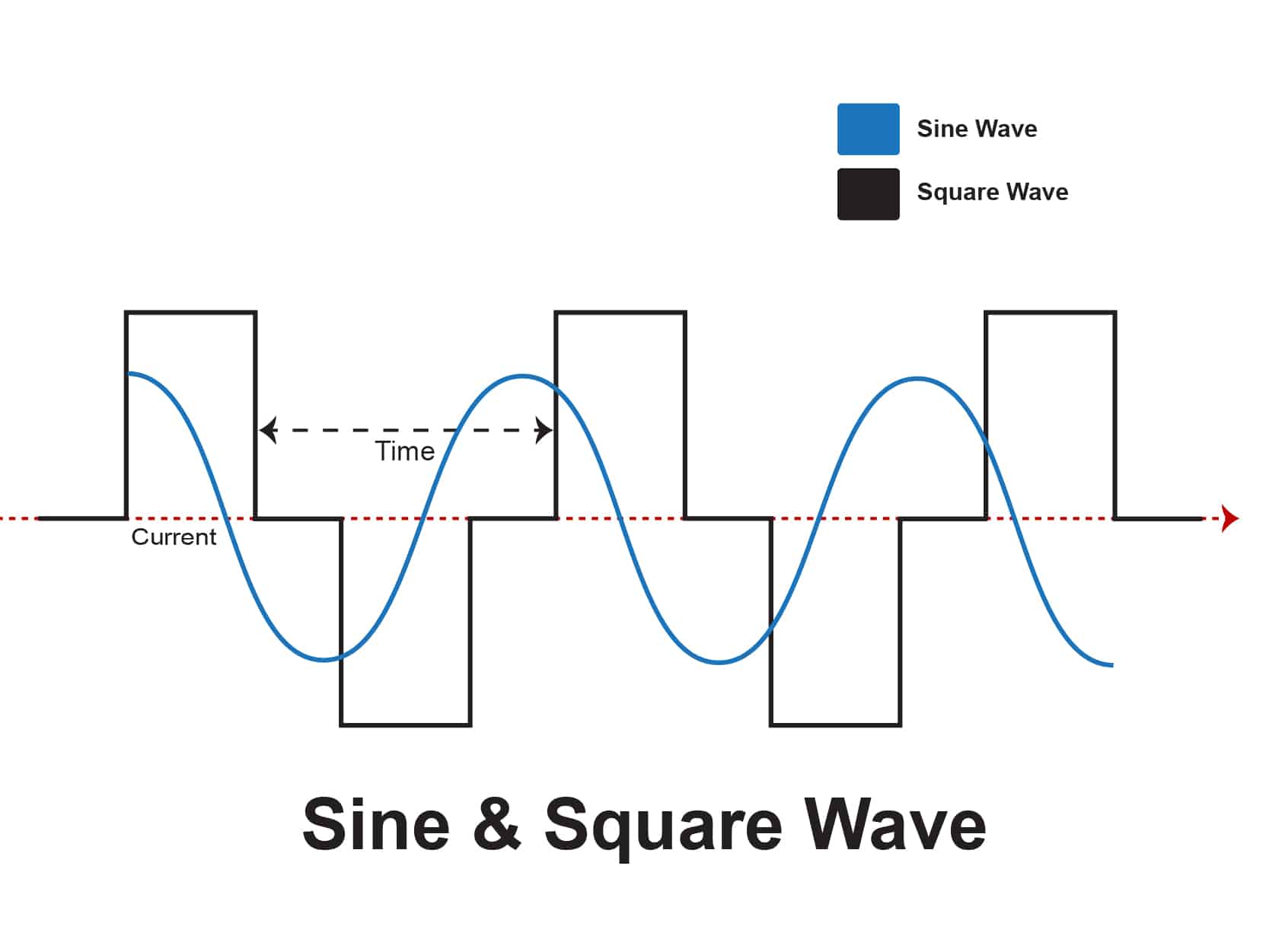
A square wave is like a light switch: it's either fully on or fully off, transitioning almost instantly between those two states. Its characterized by sharp, abrupt changes. Imagine a perfect step up, then a flat line, then immediately down. That's your ideal square wave. These are commonly found in digital circuits and timing signals.

On the other hand, a sine wave is smooth and continuous, like the gentle rolling of ocean waves. It gradually oscillates between its peak and trough, without any sudden jumps. Think of a pendulum swinging back and forth; its position over time traces a sine wave. Sine waves are fundamental to many natural phenomena, like sound waves and electromagnetic radiation.

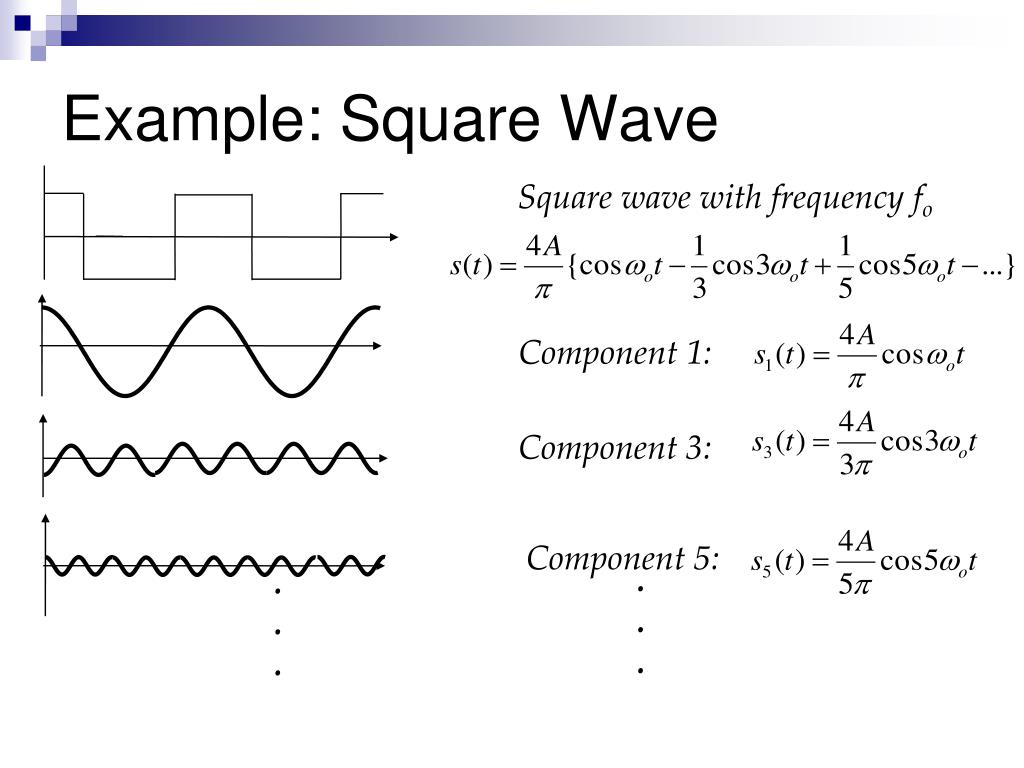
The core difference lies in their frequency components. A pure sine wave has only one frequency. A square wave, however, is composed of a fundamental frequency plus an infinite series of odd harmonics (3rd, 5th, 7th, etc.). These harmonics are sine waves with frequencies that are multiples of the fundamental, and they're what give the square wave its sharp edges. Without those harmonics, you wouldn't have a square wave at all!

The Reality of Direct Connection

2. What Happens When You Try?

Okay, so you try wiring a square wave generator directly into something expecting a sine wave. What happens? Well, it depends. If the "something" is a simple amplifier, it will probably just amplify the square wave, potentially distorting it further. The amplifier might not be able to handle the rapid transitions of the square wave, resulting in ringing or overshoot.

If you're feeding it into a more complex circuit designed specifically for sine waves (like a filter or oscillator), things get more interesting. The circuit will attempt to process the square wave's various frequency components differently. Some frequencies might be amplified, others attenuated, and the output will be a distorted mess that probably doesn't resemble either a square wave or a sine wave!

Think of it like trying to pour chunky peanut butter through a sieve designed for fine flour. The sieve will catch the chunks, and what comes out the other side won't be what you expected. Similarly, a circuit designed for sine waves won't cleanly process the harmonic content of a square wave.

In short, a direct "connection" without any signal conditioning is generally a bad idea and likely to result in unpredictable behavior. At best, you get a distorted signal; at worst, you could damage your equipment.

The Magic of Waveform Conversion

3. Transforming Squares into Sines (and Vice Versa!)

While a direct connection is usually a no-go, the good news is that you can convert a square wave into a sine wave, and vice versa. This is where signal processing techniques come into play. The key is understanding the frequency components of each waveform and using filters to shape the signal.

To convert a square wave to a sine wave, you need to remove the harmonics. This is typically done with a low-pass filter. A low-pass filter allows frequencies below a certain cutoff point to pass through while attenuating frequencies above it. By setting the cutoff frequency just above the fundamental frequency of the square wave, you can effectively filter out the higher-order harmonics, leaving you with a much cleaner sine wave approximation.

The effectiveness of this conversion depends on the quality of the filter. A sharper cutoff filter will result in a closer approximation to a pure sine wave, but even a simple RC filter can provide a noticeable improvement. You won't get a perfect sine wave, but it will be much closer than the original square wave.

Conversely, generating a square wave from a sine wave is a bit trickier, but still achievable. This can be done using a comparator circuit. A comparator compares two voltages and outputs a high voltage if one input is higher than the other, and a low voltage otherwise. By feeding a sine wave into a comparator, you can generate a square wave that switches between the high and low states at the zero crossings of the sine wave. Again, the resulting square wave won't be perfect; it will have a finite rise time, but it will generally be a good approximation.

Why Bother Converting?

4. Applications and Use Cases

You might be wondering, "Why even bother converting between square and sine waves?" Well, different applications require different types of signals. For example, many audio systems and communication systems rely on sine waves for their smooth, predictable characteristics. Square waves, on the other hand, are essential for digital circuits, timing signals, and switching power supplies.

Consider a musical instrument that generates sound electronically. The instrument might initially generate a square wave, but to produce a pleasant, musical tone, it needs to shape that square wave into a more sinusoidal waveform. This is where filters and other signal processing techniques come into play.

In telecommunications, sine waves are used as carrier signals to transmit information. Modulating a sine wave with data allows the information to be transmitted over long distances. While the data itself might be represented digitally as a square wave, it needs to be converted to a sine wave for transmission.

Furthermore, understanding the relationship between square waves and sine waves is crucial for diagnosing and troubleshooting electronic circuits. Recognizing the presence of harmonics in a square wave can help identify potential sources of noise or distortion in a system. And knowing how to filter out those harmonics can lead to improved signal quality and performance.

Practical Considerations

5. Things to Keep in Mind

Before you start experimenting with connecting and converting waveforms, there are a few practical considerations to keep in mind. First, pay attention to voltage levels. Make sure that the voltage levels of the square wave and sine wave are compatible with the circuits you're connecting them to. Overvoltage can damage components.

Second, consider impedance matching. Impedance mismatch can cause reflections and signal loss, especially at higher frequencies. Use appropriate termination resistors to minimize these effects. A good rule of thumb is to match the impedance of the source to the impedance of the load.

Third, be aware of grounding issues. Ground loops can introduce noise and interference into your circuits. Use a star grounding configuration to minimize ground loop currents. Connect all ground points to a single, central ground point to avoid creating multiple ground paths.

Finally, use appropriate test equipment. An oscilloscope is invaluable for visualizing waveforms and measuring their characteristics. A spectrum analyzer can help you analyze the frequency content of a signal. And a multimeter can be used to measure voltage levels and impedance.

FAQ

6. Your Burning Questions Answered

Still scratching your head? Here are some frequently asked questions to help clear things up:

Q: Can I use a square wave to power my home audio speakers?

A:

Technically, yes, you can, but you absolutely shouldn't. Speakers are designed to reproduce sine waves (or at least, waveforms that approximate them). Feeding a square wave directly into a speaker will likely sound terrible due to the harsh harmonics, and could potentially damage the speaker itself.

Q: What kind of filter is best for converting a square wave to a sine wave?

A:

Generally, a low-pass filter with a sharp cutoff frequency is ideal. Butterworth or Bessel filters are common choices. The sharper the cutoff, the better the sine wave approximation. Experiment to find what works best for your application!

Q: Will a perfectly filtered square wave become a perfect sine wave?

A:

Almost, but probably not perfectly. Real-world filters aren't ideal; they have imperfections and limitations. However, with a good filter design, you can get very, very close to a pure sine wave. The "perfectness" is usually more than adequate for most applications.