Lessons I Learned From Info About Is Perpendicular Bisector
Construction Angle And Perpendicular Bisectors Maths Explanation
Unlocking the Secrets of the Perpendicular Bisector
1. What Exactly IS a Perpendicular Bisector, Anyway?
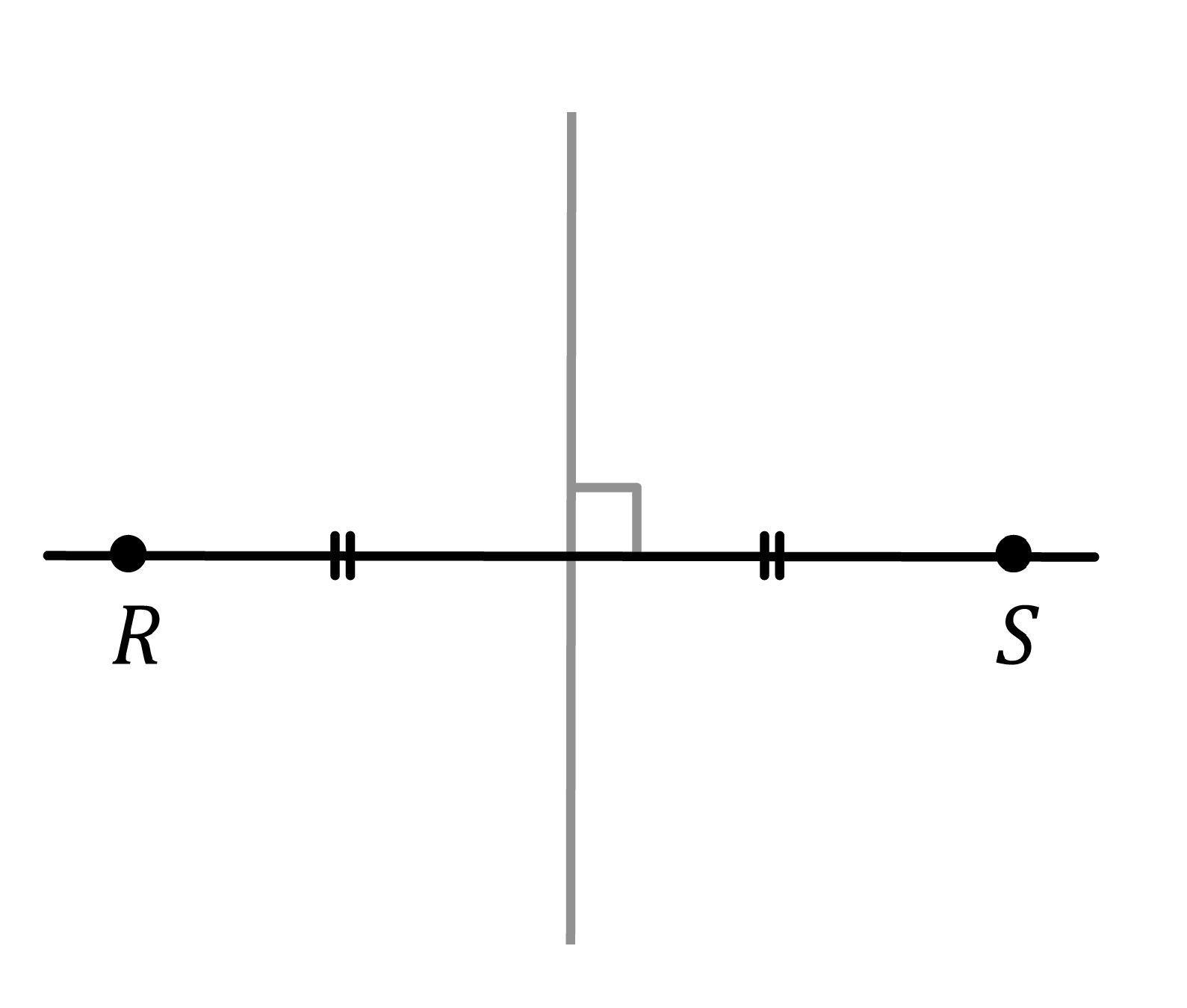
Ever heard someone mention a "perpendicular bisector" and felt a slight chill of geometry-induced dread? Don't worry, it's not as intimidating as it sounds! Think of it as a straight line that's a super-achiever. It doesn't just cross another line; it does so at a perfect 90-degree angle and cuts that line exactly in half. Like a pizza cutter thats also a protractor, but for lines. We will get into it in a sec.
The "perpendicular" part means it forms a right angle (that little square symbol you see in geometry diagrams) with the line it intersects. And the "bisector" part means it slices the line into two equal segments. So, it's like a mathematical power couple, combining perfect angles and equal divisions.
Imagine a tightrope walker. The rope is the line you want to bisect. A support beam coming straight up from the ground, perfectly at a right angle and hitting the rope in the middle, is your perpendicular bisector. If the rope is, say, 10 feet long, the bisector makes sure you have two 5-foot sections. Makes sense, right? Even tightrope walkers appreciate precise geometry!
Why is this important? Well, perpendicular bisectors pop up everywhere in geometry and beyond. They're essential for constructions, proofs, and even understanding concepts like symmetry and circles. Think of them as the unsung heroes of the geometric world, quietly keeping everything balanced and perfectly aligned. So, let's dive a little deeper and see what makes them so special.
Prove The Perpendicular Bisector Theorem
The Dynamic Duo
2. Why Both Perpendicularity and Bisection are Important
We've touched on the individual meanings of "perpendicular" and "bisector," but let's emphasize why the combination is so significant. It's like having a superhero team where each member's powers complement each other. One without the other just wouldn't be as effective.
Imagine you only have a bisector — a line that cuts another line in half, but at a random angle. It still divides the line equally, but it doesn't create any special angles or symmetry. Its just there. Not particularly helpful for precise geometric constructions.
Now, imagine you have a perpendicular line, but it doesn't bisect the original line. It creates a right angle, which is great, but it doesn't divide the line into equal segments. You get a nice corner, but no equal halves. Again, not quite the geometric powerhouse we're aiming for.
But put them together, and BAM! You get a perpendicular bisector. The perpendicularity guarantees a clean, precise right angle, and the bisection ensures perfect symmetry. This combination unlocks a whole range of possibilities in geometry, allowing us to construct circles, find centers, and prove theorems with elegance and accuracy. It's the peanut butter and jelly of geometric concepts!

Perpendicular Bisector Of A Segment In Real Life
Constructing the Perfect Perpendicular Bisector
3. Tools and Techniques for Creating Accurate Bisectors
So, how do we actually make a perpendicular bisector? There are a couple of ways, each with its own charm. The most classic method involves a compass and a straightedge (ruler without markings — geometry purists, you know). This method is elegant, precise, and surprisingly simple once you get the hang of it.
Here's the gist: Start with the line segment you want to bisect. Open your compass to a distance that's more than half the length of the segment. Place the compass point on one endpoint of the segment and draw an arc that extends above and below the line. Without changing the compass width, repeat the process from the other endpoint of the segment. The two arcs will intersect at two points.
Now, use your straightedge to draw a line through the two intersection points. Voila! You've constructed a perpendicular bisector. This line is both perpendicular to the original segment and divides it exactly in half. It's a beautiful and precise way to create this fundamental geometric element.
There's also an analytical approach if you have coordinates. Find the midpoint of the line segment (average the x-coordinates and the y-coordinates). Then, find the slope of the line segment. The slope of the perpendicular bisector will be the negative reciprocal of that slope. Use the midpoint and the new slope to write the equation of the line — that's your perpendicular bisector!

How To Draw Perpendicular Bisector Sullins Glinte
Real-World Applications
4. Beyond the Classroom
Okay, so perpendicular bisectors are cool and all, but where do they show up outside of textbooks and geometry problems? Turns out, they have some surprisingly practical applications. Think about anything that requires precise alignment or equal distribution.
Consider architecture and construction. When building a bridge or a symmetrical structure, ensuring that elements are perfectly balanced and aligned is crucial. Perpendicular bisectors can help determine center points, create symmetrical designs, and ensure structural integrity. A slightly off angle can cause a disaster down the line.
Another application is in mapmaking and navigation. Finding the shortest distance between two points or determining the center of a region often involves using perpendicular bisectors. They can also be used to construct accurate maps and navigational tools. Imagine getting lost because a cartographer didn't know their perpendicular bisectors!
Even in computer graphics and game development, perpendicular bisectors play a role. They can be used to create symmetrical objects, determine collision points, and generate realistic reflections. So, the next time you're playing a video game with stunning graphics, remember to thank the humble perpendicular bisector.
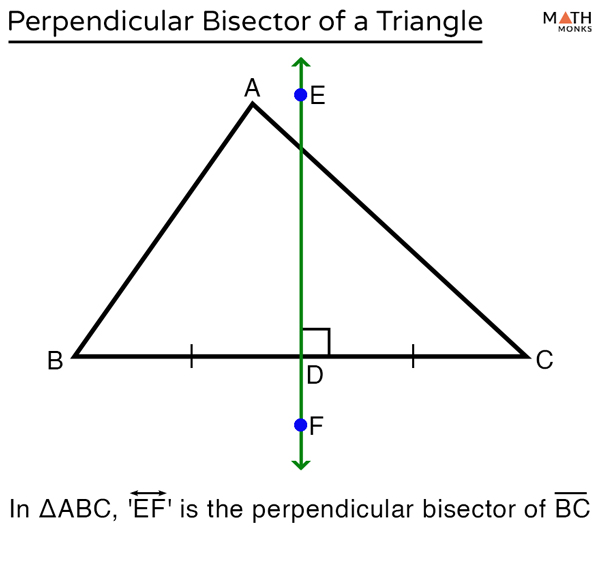
Perpendicular Bisectors and Circles
5. How Bisectors Relate to Circles
Circles and perpendicular bisectors have a special relationship, almost like they're best friends in the world of geometry. This relationship is particularly useful for finding the center of a circle, even if you only have a small arc of the circle to work with. Knowing the center makes calculating radius, circumference, and area easy!
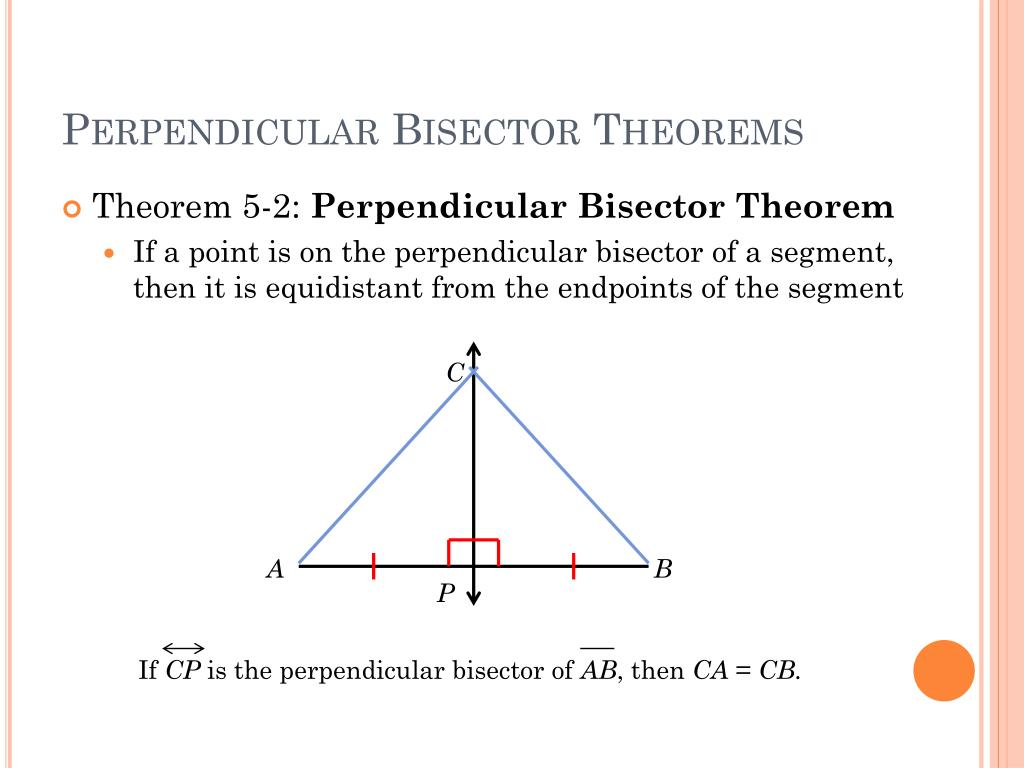
Here's how it works: draw any two chords (line segments that connect two points on the circle) on the circle. Then, construct the perpendicular bisector of each chord. The point where these two perpendicular bisectors intersect is the center of the circle. Simple, right?
Why does this work? Because every point on the perpendicular bisector of a chord is equidistant from the endpoints of that chord. And since the center of a circle is equidistant from all points on the circle, it must lie on the perpendicular bisector of any chord. Therefore, the intersection of two perpendicular bisectors pinpoints the exact center.
This principle is often used in engineering and design when dealing with circular objects. For instance, if you need to find the center of a pipe or a wheel, you can use this method to locate it accurately, even if you can't see the entire circle. So, remember, when in doubt, bisect those chords!

Frequently Asked Questions (FAQs) About Perpendicular Bisectors
6. Your Burning Questions Answered!
Let's tackle some of the common questions that people have about perpendicular bisectors.
Q: Is a median of a triangle always a perpendicular bisector?
A: Not necessarily! A median of a triangle only connects a vertex to the midpoint of the opposite side. It doesn't have to be perpendicular to that side. Only in specific types of triangles (like isosceles or equilateral triangles) will a median also be a perpendicular bisector.
Q: Can I use a protractor to draw a perpendicular bisector?
A: Yes, you can! Use the protractor to create a line at a 90-degree angle to the line segment. Then, measure half the length of the segment from the intersection point in both directions. This method is less precise than using a compass and straightedge, but it can be helpful in a pinch.
Q: Are perpendicular bisectors always unique for a given line segment?
A: Yes, there is only one unique perpendicular bisector for any given line segment. It's defined by both its perpendicularity and its bisection properties, leaving no room for other lines to fit the criteria.